Mathematical Modeling

1  Why mathematical modeling?

Mathematical modeling is the art of translating problems from an application area into tractable mathematical formulations whose theoretical and numerical analysis provides insight, answers, and guidance useful for the originating application.

Mathematical modeling

• is indispensable in many applications

• is successful in many further applications

• gives precision and direction for problem solution

• enables a thorough understanding of the system modeled

• prepares the way for better design or control of a system

• allows the efficient use of modern computing capabilities

Learning about mathematical modeling is an important step from a theoretical mathematical training to an application-oriented mathematical expertise, and makes the student fit for mastering the challenges of our modern technological culture.

2  A list of applications

In the following, I give a list of applications whose modeling I understand, at least in some detail. All areas mentioned have numerous mathematical challenges.

This list is based on my own experience; therefore it is very incomplete as a list of applications of mathematics in general. There are an almost endless number of other areas with interesting mathematical problems.

Indeed, mathematics is simply the language for posing problems precisely and unambiguously (so that even a stupid, pedantic computer can understand it).

Anthropology

• Modeling, classifying and reconstructing skulls

Archeology

• Reconstruction of objects from preserved fragments

• Classifying ancient artifices

Architecture

• Virtual reality

Artificial intelligence

• Computer vision

• Image interpretation

• Robotics

• Speech recognition

• Optical character recognition

• Reasoning under uncertainty

Arts

• Computer animation (Jurassic Park)

Astronomy

• Detection of planetary systems

• Correcting the Hubble telescope

• Origin of the universe

• Evolution of stars

Biology

• Protein folding

• Humane genome project

• Population dynamics

• Morphogenesis

• Evolutionary pedigrees

• Spreading of infectuous diseases (AIDS)

• Animal and plant breeding (genetic variability)

Chemical engineering

• Chemical equilibrium

• Planning of production units

Chemistry

• Chemical reaction dynamics

• Molecular modeling

• Electronic structure calculations

Computer science

• Image processing

• Realistic computer graphics (ray tracing)

Criminalistic science

• Finger print recognition

• Face recognition

Economics

• Labor data analysis

Electrical engineering

• Stability of electric curcuits

• Microchip analysis

• Power supply network optimization

Finance

• Risk analysis

• Value estimation of options

Fluid mechanics

• Wind channel

• Turbulence

Geosciences

• Prediction of oil or ore deposits

• Map production

• Earth quake prediction

Internet

• Web search

• Optimal routing

Linguistics

• Automatic translation

Materials Science

• Microchip production

• Microstructures

• Semiconductor modeling

Mechanical engineering

• Stability of structures (high rise buildings, bridges, air planes)

• Structural optimization

• Crash simulation

Medicine

• Radiation therapy planning

• Computer-aided tomography

• Blood circulation models

Meteorology

• Weather prediction

• Climate prediction (global warming, what caused the ozone hole?)

Music

• Analysis and synthesis of sounds

Neuroscience

• Neural networks

• Signal transmission in nerves

Pharmacology

• Docking of molecules to proteins

• Screening of new compounds

Physics

• Elementary particle tracking

• Quantum field theory predictions (baryon spectrum)

• Laser dynamics

Political Sciences

• Analysis of elections

Psychology

• Formalizing diaries of therapy sessions

Space Sciences

• Trajectory planning

• Flight simulation

• Shuttle reentry

Transport Science

• Air traffic scheduling

• Taxi for handicapped people

• Automatic pilot for cars and airplanes

3  Basic numerical tasks

The following is a list of categories containing the basic algorithmic toolkit needed for extracting numerical information from mathematical models.

Due to the breadth of the subject, this cannot be covered in a single course. For a thorough education one needs to attend courses (or read books) at least on numerical analysis (which usually covers some numerical linear algebra, too), optimization, and numerical methods for partial differential equations.

Unfortunately, there appear to be few good courses and books on (higher-dimensional) numerical data analysis.

Numerical linear algebra

• Linear systems of equations

• Eigenvalue problems

• Linear programming (linear optimization)

• Techniques for large, sparse problems

Numerical analysis

• Function evaluation

• Automatic and numerical differentiation

• Interpolation

• Approximation (Padé, least squares, radial basis functions)

• Integration (univariate, multivariate, Fourier transform)

• Special functions

• Nonlinear systems of equations

• Optimization = nonlinear programming

• Techniques for large, sparse problems

Numerical data analysis (= numerical statistics)

• Visualization (2D and 3D computational geometry)

• Parameter estimation (least squares, maximum likelihood)

• Prediction

• Classification

• Time series analysis (signal processing, filtering, time correlations, spectral analysis)

• Categorical time series (hidden Markov models)

• Random numbers and Monte Carlo methods

• Techniques for large, sparse problems

Numerical functional analysis

• Ordinary differential equations (initial value problems, boundary value problems, eigenvalue problems, stability)

• Techniques for large problems

• Partial differential equations (finite differences, finite elements, boundary elements, mesh generation, adaptive meshes)

• Stochastic differential equations

• Integral equations (and regularization)

Non-numerical algorithms

• Symbolic methods (computer algebra)

• Sorting

• Compression

• Cryptography

• Error correcting codes

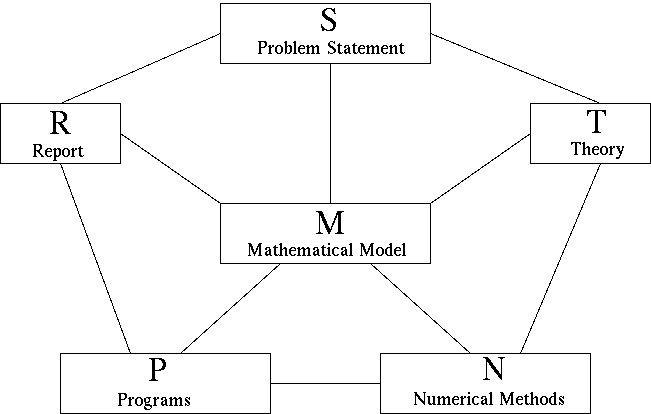
4  The modeling diagram

The nodes of the following diagram represent information to be collected, sorted, evaluated, and organized.

The edges of the diagram represent activities of two-way communication (flow of relevant information) between the nodes and the corresponding sources of information.

S. Problem Statement

• Interests of customer/boss

• Often ambiguous/incomplete

• Wishes are sometimes incompatible

M. Mathematical Model

• Concepts/Variables

• Relations

• Restrictions

• Goals

• Priorities/Quality assignments

T. Theory

• of Application

• of Mathematics

• Literature search

N. Numerical Methods

• Software libraries

• Free software from WWW

• Background information

P. Programs

• Flow diagrams

• Implementation

• User interface

• Documentation

R. Report

• Description

• Analysis

• Results

• Validation

• Visualization

• Limitations

• Recommendations

Using the modeling diagram

• The modeling diagram breaks the modeling task into 16=6+10 different processes.

• Each of the 6 nodes and each of the 10 edges deserve repeated attention, usually at every stage of the modeling process.

• The modeling is complete only when the 'traffic' along all edges becomes insignificant.

• Generally, working on an edge enriches both participating nodes.

• If stuck along one edge, move to another one! Use the general rules below as a check list!

• Frequently, the problem changes during modeling, in the light of the understanding gained by the modeling process. At the end, even a vague or contradictory initial problem description should have developed into a reasonably well-defined description, with an associated precisely defined (though perhaps inaccurate) mathematical model.

5  General rules

• Look at how others model similar situations; adapt their models to the present situation.

• Collect/ask for background information needed to understand the problem.

• Start with simple models; add details as they become known and useful or necessary.

• Find all relevant quantities and make them precise.

• Find all relevant relationships between quantities ([differential] equations, inequalities, case distinctions).

• Locate/collect/select the data needed to specify these relationships.

• Find all restrictions that the quantities must obey (sign, limits, forbidden overlaps, etc.). Which restrictions are hard, which soft? How soft?

• Try to incorporate qualitative constraints that rule out otherwise feasible results (usually from inadequate previous versions).

• Find all goals (including conflicting ones)

• Play the devil's advocate to find out and formulate the weak spots of your model.

• Sort available information by the degree of impact expected/hoped for.

• Create a hierarchy of models: from coarse, highly simplifying models to models with all known details. Are there useful toy models with simpler data? Are there limiting cases where the model simplifies? Are there interesting extreme cases that help discover difficulties?

• First solve the coarser models (cheap but inaccurate) to get good starting points for the finer models (expensive to solve but realistic)

• Try to have a simple working model (with report) after 1/3 of the total time planned for the task. Use the remaining time for improving or expanding the model based on your experience, for making the programs more versatile and speeding them up, for polishing documentation, etc.

• Good communication is essential for good applied work.

• The responsibility for understanding, for asking the questions that lead to it, for recognizing misunderstanding (mismatch between answers expected and answers received), and for overcoming them lies with the mathematician. You cannot usually assume your customer to understand your scientific jargon.

• Be not discouraged. Failures inform you about important missing details in your understanding of the problem (or the customer/boss) - utilize this information!

• There are rarely perfect solutions. Modeling is the art of finding a satisfying compromise. Start with the highest standards, and lower them as the deadline approaches. If you have results early, raise your standards again.

• Finish your work in time.

Lao Tse: ''People often fail on the verge of success; take care at the end as at the beginning, so that you may avoid failure.''

6  Conflicts

Most modeling situations involve a number of tensions between conflicting requirements that cannot be reconciled easily.

• fast - slow

• cheap - expensive

• short term - long term

• simplicity - complexity

• low quality - high quality

• approximate - accurate

• superficial - in depth

• sketchy - comprehensive

• concise - detailed

• short description - long description

Einstein: ''A good theory'' (or model) ''should be as simple as possible, but not simpler.''

• perfecting a program - need for quick results

• collecting the theory - producing a solution

• doing research - writing up

• quality standards - deadlines

• dreams - actual results

The conflicts described are creative and constructive, if one does not give in too easily. As a good material can handle more physical stress, so a good scientist can handle more stress created by conflict.

''We shall overcome'' - a successful motto of the black liberation movement, created by a strong trust in God. This generalizes to other situations where one has to face difficulties, too.

Among other qualities it has, university education is not least a long term stress test - if you got your degree, this is a proof that you could overcome significant barriers. The job market pays for the ability to persist.

7  Attitudes

• Do whatever you do with love. Love (even in difficult circumstances) can be learnt; it noticeably improves the quality of your work and the satisfaction you derive from it.

• Do whatever you do as a service to others. This will improve your attention, the feedback you'll get, and the impact you'll have.

• Take responsibility; ask if in doubt; read to confirm your understanding. This will remove many impasses that otherwise would delay your work.

Jesus: ''Ask, and you will receive. Search, and you will find. Knock, and the door will be opened for you.''

8  References

For more information about mathematics, software, and applications, see, e.g., my home page, at http://arnold-neumaier.at/